Unit cell transformation

IrRep is able to calculate the traces of symmetry operations regardless of the unit cell used for the DFT calculation, but if we also want to determine the irreducible representations at maximal k-points, IrRep will need the transformation from the DFT cell to the conventional cell in which the tables of irreps are written. Even though IrRep is able to calculate the transformation automatically, the user can specify the transformation via the input parameters refUC and shiftUC.

Here, we first show how the parameters refUC and shiftUC can be used to provide IrRep with the unit cell transformation. After that, we will set the notation related to the tranformation of the unit cell that is followed internally in IrRep, which may be interesing for developers.

How to specify the transformation

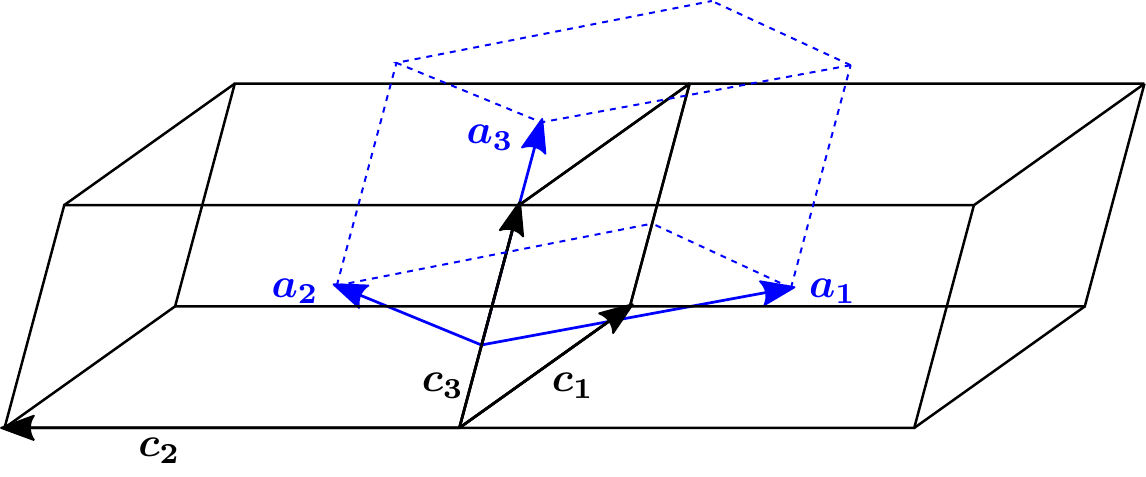
Let \((\boldsymbol{a_1}, \boldsymbol{a_2}, \boldsymbol{a_3})\) be the basis vectors of the DFT cell and \((\boldsymbol{c_1}, \boldsymbol{c_2}, \boldsymbol{c_3})\) the basis vectors of the conventional cell. The parameter refUC is the matrix that describes the transformation between the basis vectors of both settings:

(1)\[\begin{split} \begin{pmatrix} \boldsymbol{c_1} \\ \boldsymbol{c_2} \\ \boldsymbol{c_3} \end{pmatrix} = refUC \cdot \begin{pmatrix} \boldsymbol{a_1} \\ \boldsymbol{a_2} \\ \boldsymbol{a_3} \end{pmatrix}\end{split}\]

For example, we could set -refUC=1,1,0,-1,1,0,0,0,1 for the case of the C-centered monoclinic structure shown in the figure below.

The parameter shiftUC describes the shift of the origin of the conventional cell with respect to its location in the DFT setting. This shift is given in terms of the basis vectors of the DFT cell. In the example of the C-centered structure, the shift is \(0.3 \boldsymbol{a_3}\), thus -shiftUC=0,0,0.3.

Definitions and notation in the code

In this section, we set the definitions and notation for the unit cell transformation that are followed internally in IrRep. This information might be interesting for potential developers and people looking into the code. Users that are not interested in these aspects are encouraged to restrict themselves to How to specify the transformation.

Let us keep on denoting \((\boldsymbol{a_1}, \boldsymbol{a_2}, \boldsymbol{a_3})\) the basis vectors of the DFT cell and \((\boldsymbol{c_1}, \boldsymbol{c_2}, \boldsymbol{c_3})\) those of the conventional cell. The transformation from the DFT cell to the conventional setting is expressed by the matrix-vector pair \((P,\boldsymbol{p})\). The matrix \(P\) describes the relation between the basis vectors in both settings:

(2)\[ (\boldsymbol{c_1}, \boldsymbol{c_2}, \boldsymbol{c_3}) = (\boldsymbol{a_1}, \boldsymbol{a_2}, \boldsymbol{a_3}) \cdot P.\]

Note that \(P\) is not identical to the matrix specified by the user via refUC; one is the transpose of the other: \(refUC=P^t\). Indeed, when the user specifies \(refUC\) in the command-line, IrRep converts it to \(P\) by taking the transpose and goes on to work with \(P\). Therefore, the notation in Eq.(1) is used only to parsing the transformation from the command-line and to printing it for the user.

The vector \(\boldsymbol{p}\) describes the position at which the origin of the conventional cell sits with respect to its location in the DFT cell, i.e. the shift of the origin. If \(O_c\) denotes the origin in the conventional cell and \(O_{DFT}\) in the DFT cell, then

\[\boldsymbol{p} = O_c - O_{DFT}.\]

\(\boldsymbol{p}\) is written in terms of the vectors of the DFT cell, thus \(\boldsymbol{p}\) and shiftUC coincide.

In the following, we will show how the expressions for vectors in real and reciprocal space and the description of symmetry operations change with the transformation of the unit cell. The equations inside boxes are implemented in the source code of IrRep literally.

Vectors in real space

It is important to realize that the unit cell transformation we are considering here does not act on the crystal, but only on the basis of vectors that we adopt to describe it. In the same spirit, a point in the unit cell does not change under the transformation, only its description does.

Let \(\boldsymbol{r}\) be a vector pointing at a position in the unit cell. It can be written in the following way, in terms of the basis vectors of the DFT cell:

\[\boldsymbol{r} = \sum_{i=1}^{3} x_i \boldsymbol{a_i},\]

It can also be expressed in terms of the basis vectors of the conventional cell, by means of the coordinates \(x'_i\):

(3)\[\boldsymbol{r} = \sum_{i=1}^{3} x'_i \boldsymbol{c_i}.\]

Let us apply the transformation Eq.(2) in this equation:

(4)\[\boldsymbol{r} = \sum_{i=1}^{3} x'_i \sum_{j=1}^{3} P_{ji} \boldsymbol{a_i} = \sum_{j=1}^{3} \sum_{i=1}^{3} P_{ji} x'_{i} \boldsymbol{c_j}.\]

As we have mentioned above, the vector \(\boldsymbol{r}\) can not change under the transformation of the unit cell, thus Eq.(3) and (4) must match, which requires \(P_{ji} x'_i = x_j\) or, equivalently, \([P^{-1}]_{ij} x'_j = x_i\).

Deriving the effect of the shift on the coordinates \(\boldsymbol{p}\) is simple. It might be helpful to think how the transformation acts when \(P=\mathbb{1}\). We conclude that, the coordinates of vectors in real space change according to the following expression under the transformation \((P,\boldsymbol{p})\) from the DFT to the conventional setting:

(5)\[\boxed{ x' = (P, \boldsymbol{p})^{-1} x}\]

where \((P, \boldsymbol{p})^{-1} = (P^{-1}, -P^{-1} \boldsymbol{p})\) is the inverse of \((P, \boldsymbol{p})\). For the sake of clarity, let us write the same expression in matrix form:

\[\begin{split}\begin{pmatrix} x'_1 \\ x'_2 \\ x'_3 \end{pmatrix} = P^{-1} \cdot \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix} - P^{-1} \cdot \begin{pmatrix} p_1 \\ p_2 \\ p_3 \end{pmatrix}.\end{split}\]

Reciprocal space basis vectors

The real and reciprocal space basis vectors are tightly related. As a consequence, when we change the real-space unit cell, the reciprocal-space cell will change with it. We now show how the reciprocal-space basis vectors change when considering the transormation \((P, \boldsymbol{p})\).

Let us denote as \((\boldsymbol{k_1}, \boldsymbol{k_2}, \boldsymbol{k_3})\) and \((\boldsymbol{q_1}, \boldsymbol{q_2}, \boldsymbol{q_3})\) the reciprocal-space basis vectors in the DFT and conventional settings, respectively. Furthermore, let us consider that these vectors are related via a matrix \(R\) in the following way:

(6)\[\boldsymbol{q_i} = R_{ji} \boldsymbol{k_j},\]

and let us determine \(R\) in terms of \(P\). For that, remember that the real and reciprocal-space basis vectos are related as \(\boldsymbol{k_i} \cdot \boldsymbol{a_j} = 2 \pi \delta_{ij}\), which also holds in the conventional settings, \(\boldsymbol{q_i} \cdot \boldsymbol{c_j} = 2 \pi \delta_{ij}\). Let us apply Eq.(2) and (6):

\[\boldsymbol{q}_i \cdot \boldsymbol{c}_j = \sum_{n,m=1}^{3} R_{mi} \boldsymbol{k_m} \cdot \boldsymbol{a_n} P_{nj} = 2 \pi \sum_{m=1}^{3} R_{mi} P_{mj} = 2 \pi \sum_{m=1}^{3} [R^t]_{im}P_{mj}.\]

As we said, this should be equal to \(2 \pi \delta_{ij}\), which requires \(R = [P^t]^{-1}\). Therefore,

(7)\[\boxed{ \boldsymbol{q_i} = \sum_{j=1}^3 [P^{-1}]_{ij} \boldsymbol{k_j}}\]

Vectors in reciprocal space

A vector \(\boldsymbol{k}\) defined in reciprocal space can be expanded in term of the basis vectors of the DFT cell: \(\boldsymbol{k} = \sum_{i=1}^{3} g_i \boldsymbol{k_i}\). It can also be written in terms of the basis vectors of the conventional setting as \(\boldsymbol{k} = \sum_{i=1}^{3} g'_i \boldsymbol{q_i}\). Let us apply Eq.(7) in the later expansion:

(8)\[ \boldsymbol{k} = \sum_{i=1}^{3} g'_i \sum_{j=1}^{3} [P^{-1}]_{ij} \boldsymbol{k_j} = \sum_{j=1}^{3} \sum_{i=1}^{3} [P^{-1}]_{ij} g'_{i} \boldsymbol{k_j}.\]

\(\boldsymbol{k}\) can not change under a unit cell transformation, only its description does. Therefore, Eq.(8) should match with the expansion in terms of the basis vectors of the DFT setting, which requires \([P^{-1}]_{ij} g'_i = g_j\) or, equivalently,

\[\boxed{ g'_i = [P^t]_{ij} g_j }\]

Action on symmetry operations

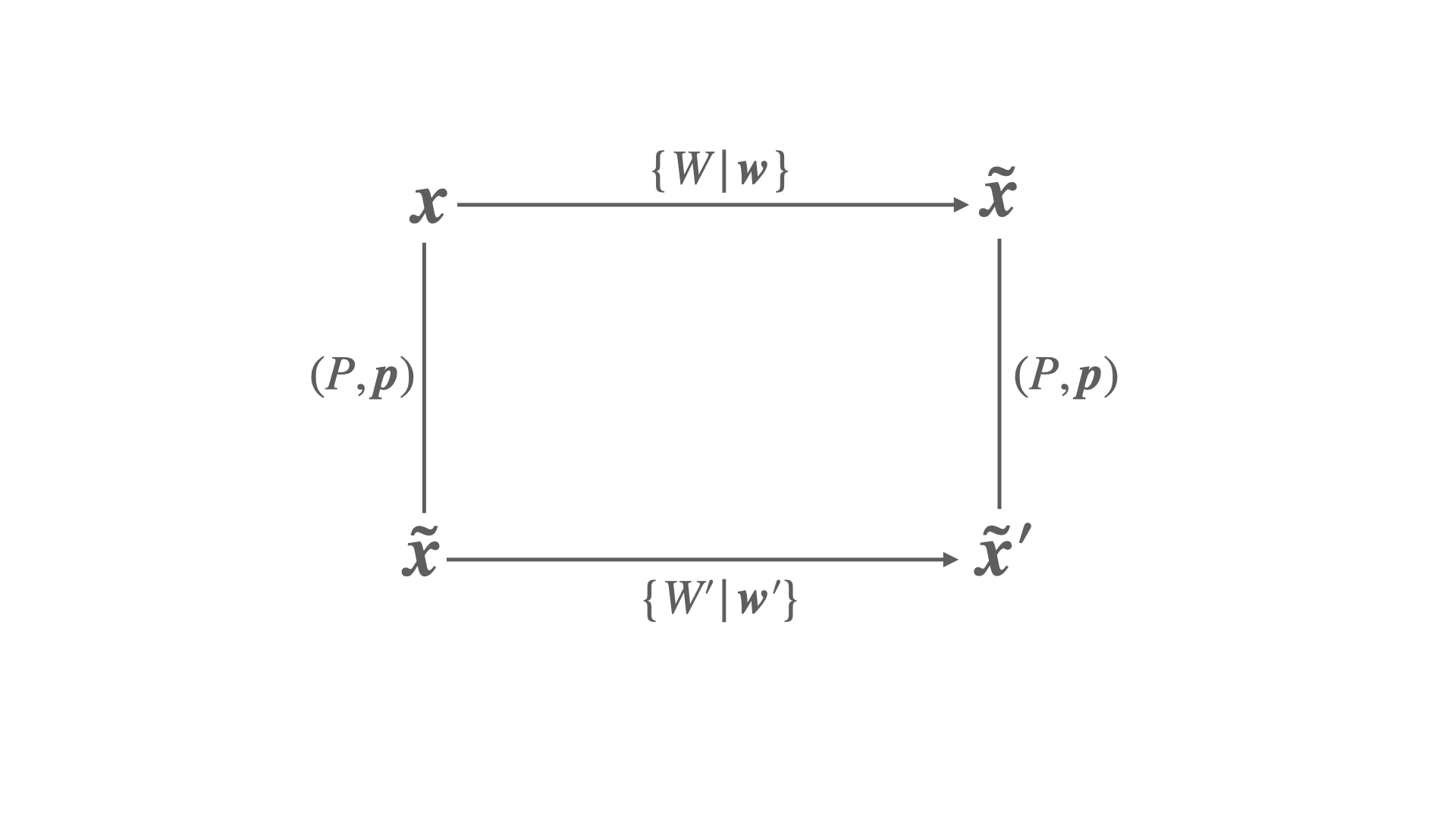
To determine the effect of a cell transformation on a symmetry operation we need to realize that they are different things. As we said, a unit cell transformation does not have any influence on the crystal–what changes is just our way of making reference to points in it. On the other hand, a symmetry operations moves atoms around in such a way that, their final arrangement is equivalent (but not indetical) to the one at the beginning. In mathematical terms, a symmetry operation \(\{ W | \boldsymbol{w} \}\) acts on a position \(\boldsymbol{r} = \sum_{i=1}^{3} x_i \boldsymbol{a_i}\) in the following way:

\[\boldsymbol{\tilde r} = \{W|\boldsymbol{w}\} \boldsymbol{r} = \sum_{i,j=1}^3 ( W_{ij} x_j + w_i ) \boldsymbol{a_i} = \sum_{i=1}^3 \tilde x_i \boldsymbol{a_i},\]

Note that the symmetry operation acts only on the coefficients of the expansion [1], whereas the unit cell transformation changes both, the coefficients and the basis vectors, such that the expansion of the vector is left invariant.

[1]

We could equivalently consider that the symmetry acts on the basis vectors, rather than on the coefficients of the expansion.

Let us denote \(\boldsymbol{\tilde x}\) the coefficients of the expansion after the unit cell transformation, i.e. \(\boldsymbol{\tilde x} = (P,\boldsymbol{p})^{-1} \boldsymbol{x}\), according to Eq.(5). The coefficients \(\boldsymbol{\tilde x}'\) in the figure above can be written as:

(9)\[\boldsymbol{\tilde x}' = \{W'| \boldsymbol{w}'\} \boldsymbol{x}',\]

where \(\{W'| \boldsymbol{w}\}\) is the symmetry operation in the conventional setting. On the other hand, the same set of coefficients can be reached by following a different way:

(10)\[ \boldsymbol{\tilde x}' = (P,\boldsymbol{p})^{-1} \boldsymbol{\tilde x} = (P,\boldsymbol{p})^{-1} \{ W,\boldsymbol{w} \} \boldsymbol{x} = (P,\boldsymbol{p})^{-1} \{W,\boldsymbol{w}\} (P,\boldsymbol{p}) \boldsymbol{x}'.\]

Since Eq.(9) and (10) must be compatible:

\[\boxed{ \{ W', \boldsymbol{w}' \} = (P,\boldsymbol{p})^{-1} \{W,\boldsymbol{w}\} (P,\boldsymbol{p}) = (P^{-1} W P, P^{-1}\boldsymbol{w}-P^{-1}\boldsymbol{p}+P^{-1}W\boldsymbol{p}) }\]